Residual Networks

Residual Networks#

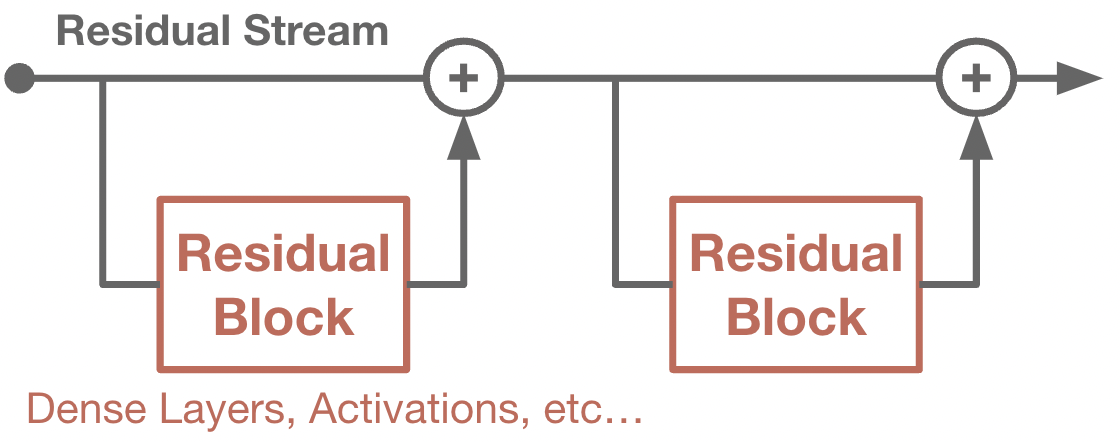
In a residual network, new features are added to previous features, instead of replacing them fully.

Deeper neural networks have the potential to become more powerful. They can perform more computation, and build off more abstract features. However, deeper networks also become harder to train. There are potential issues with vanishing or exploding gradients, in which certain badly-behaved layers can corrupt the learning signal for the entire network. A sneakier issue is that of a chicken-and-egg problem – when later layers have not been properly trained, they will inhibit the earlier layers from learning relevant features.

Residual networks add an explicit bias towards preserving prior information. In a residual network, we view the main information flow as the residual stream. Each additional layer does not completely rewrite the residual stream, but instead inserts new information into it. Thus, by default, information from prior layers is retained into later layers. We often group operations that read/write from the stream into residual blocks. Residual networks are known to ease optimization, and provide shorter gradient flows between the intermediate features and signal from the loss function.

class MyResidualLayer(nn.Module):
    @nn.compact
    def __call__(self, x):
        # Residual block: Perform some computation. Here we use two dense layers.
        y = nn.Dense(features=128)(x)
        y = nn.relu(y)
        y = nn.Dense(features=128)(y)
        return x + y # Add new features to residual stream.

Is there a difference between a residual layer and a dense layer with the right parameters?#

If the input and output spaces of the residual block are the same, then the residual connection is does not create any unique structure. It is possible to achieve the same residual effect by simply utilzing a parameter matrix that has a constant weight along the diagonal, which preserves the input features. However, even in this setting, the residual connection can be a powerful inductive bias. Residual layers will by default place a large emphasis on preserving the input, a behavior which otherwise is not present at random initialization.

What are numerical benefits of a residual connection?#

In deep learning, we sometimes worry about network collapse. A common measurement is rank collapse, which occurs when a dense layer aligns its parameters such that the outputs become lower rank than the inputs. In a regular dense network, rank collapse cannot be undone – once the information is lost, later layers cannot recover the information. However, in a residual network, even if a single layer exhibits rank collapse, the residual stream itself will retain its full-rank structure, as the previous features will remain unmodified.

Residual layers can also cause better gradient flow. In a residual network, gradients are backpropagated through the residual stream. This causes any intermediate layer to have a close-to-direct path to the loss function.

Should we normalize along the residual stream?#

In general, no. Normalization tends to harm the gradient flow and slow down learning. In typical architectures, we will use normalization layers within each residual block, but the main residual stream will be untouched.

Example: U-Net Architecture#

A well-known residual architecture in image generation is the U-Net. In image generation, our input and output spaces are both full images. However, we want to progressively downsample these images within the network, as is typically done in convolutional architectures. The downside here is that we lose the high-frequency details present in the original image. The U-Net architecture uses residual connections between each resolution, allowing for information to flow back to the original image at various resolutions.

Unet

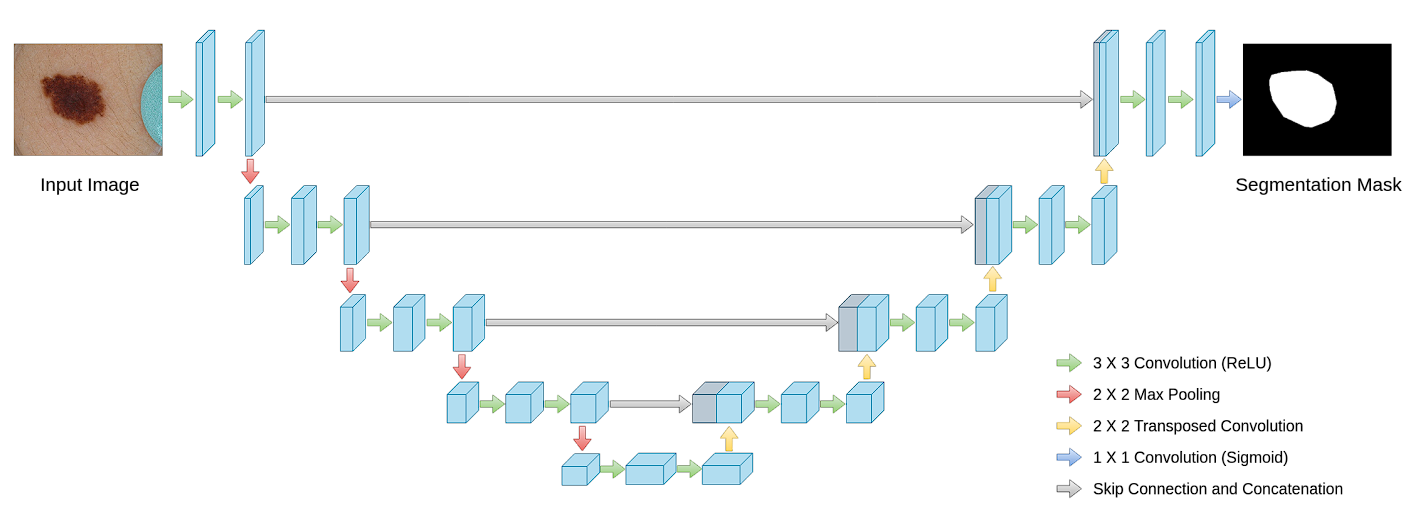
Source: Ibtehaz et al. A typical U-Net. “Skip connection” is equivalent to residual connection.